삼각 함수의 덧셈 정리의 증명

 삼각 함수의 덧셈 정리의 두 가지 증명입니다.

 

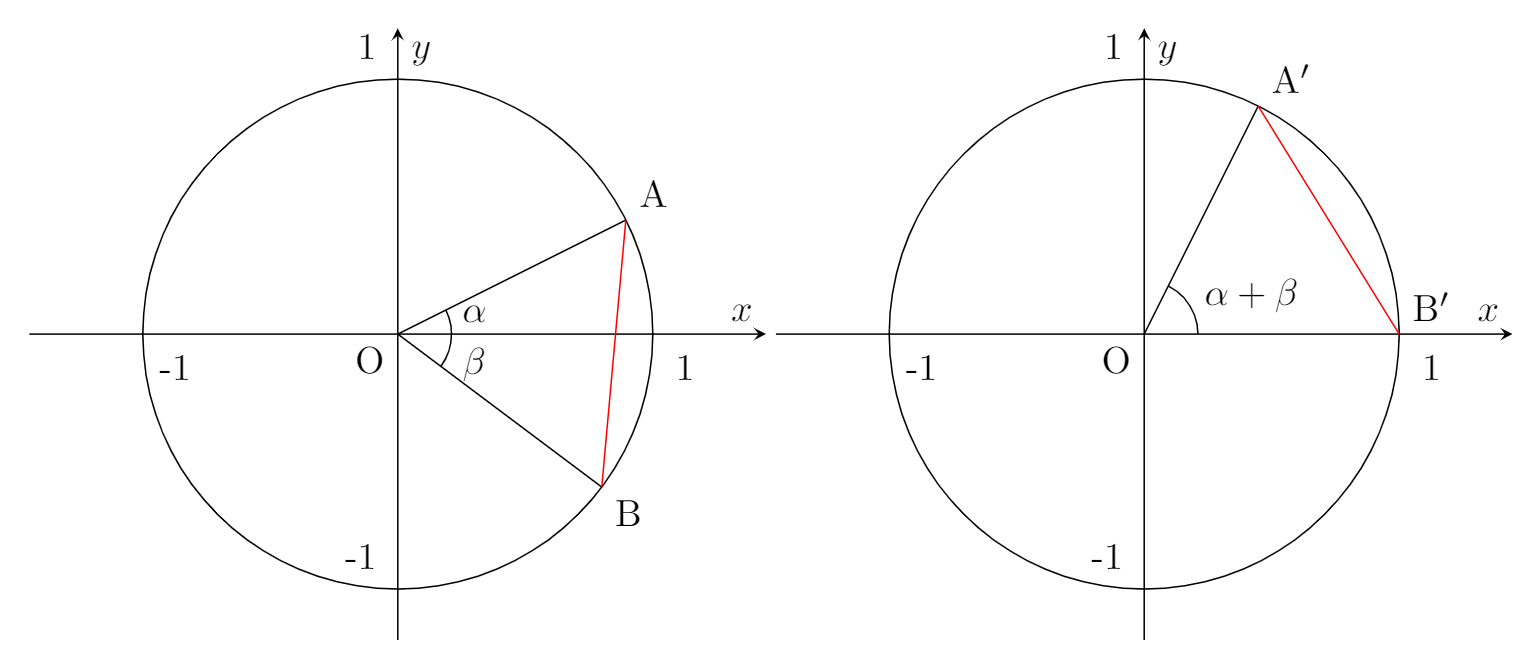
 위 두 그림에서 빨간색으로 표시된 $\overline{\mathrm{AB}}=\overline{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}$임을 이용합니다. $\mathrm{△}\mathrm{OAB}\equiv \mathrm{△}{\mathrm{OA}}^{\prime }{\mathrm{B}}^{\prime }$ (SAS 합동)이기 때문입니다.

$$\mathrm{A}(\cos \alpha ,\sin \alpha ),\mathrm{B}(\cos \beta ,\sin \beta )$$

$$\begin{array}{rl}{\overline{\mathrm{AB}}}^2& =(\cos \alpha -\cos \beta {)}^2+(\sin \alpha +\sin \beta {)}^2\\ & =2-2\cos \alpha \cos \beta +2\sin \alpha \sin \beta \end{array}$$

$${\mathrm{A}}^{\prime }(\cos (\alpha +\beta ),\sin (\alpha +\beta )),{\mathrm{B}}^{\prime }(1,0)$$

$$\begin{array}{rl}{\overline{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}}^2& =(\cos (\alpha +\beta )-1{)}^2+{\sin }^2(\alpha +\beta )\\ & =2-2\cos (\alpha +\beta )\end{array}$$

$$\therefore 2-2\cos \alpha \cos \beta +2\sin \alpha \sin \beta =2-2\cos (\alpha +\beta )$$

$$\therefore \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$$

 

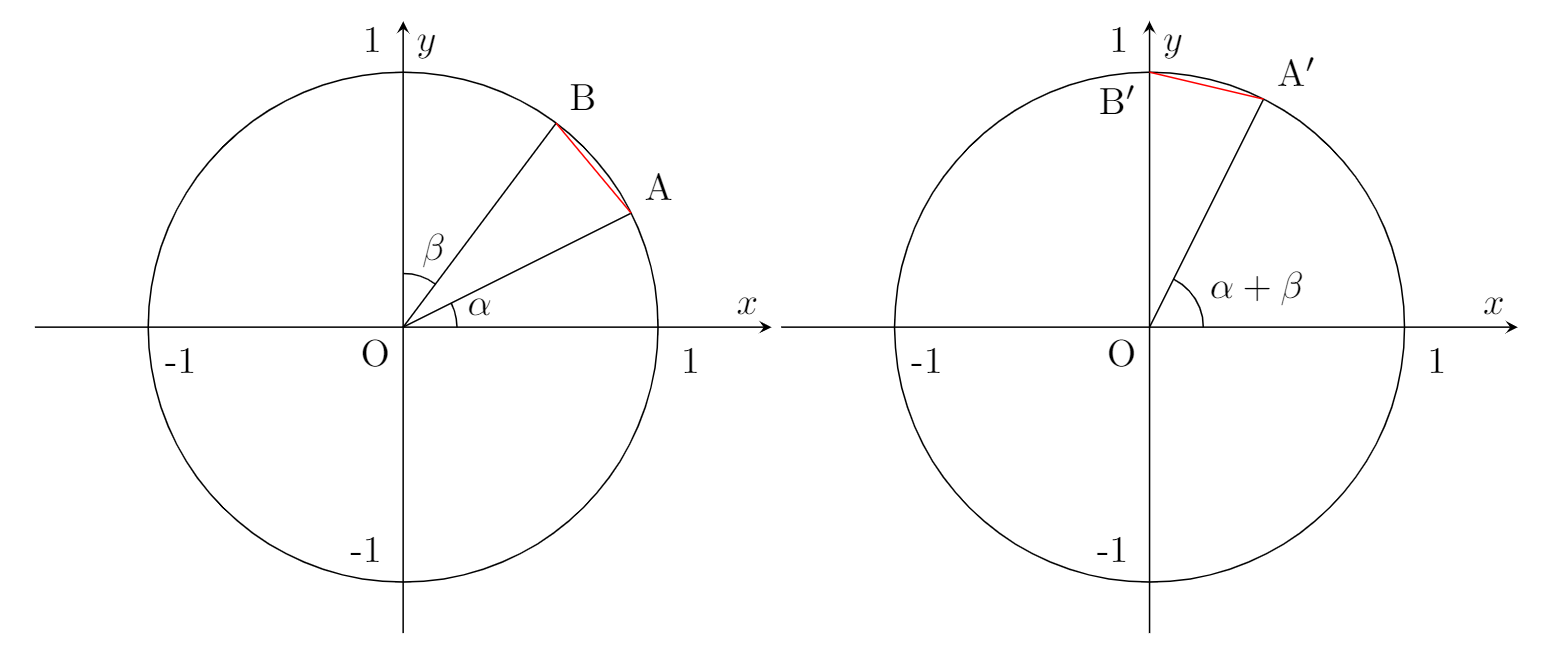
 또, 위 두 그림에서 빨간색으로 표시된 $\overline{\mathrm{AB}}=\overline{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}$임을 이용합니다. 마찬가지로 $\mathrm{△}\mathrm{OAB}\equiv \mathrm{△}{\mathrm{OA}}^{\prime }{\mathrm{B}}^{\prime }$ (SAS 합동)이기 때문입니다.

$$\mathrm{A}(\cos \alpha ,\sin \alpha ),\mathrm{B}(\sin \beta ,\cos \beta )$$

$$\begin{array}{rl}{\overline{\mathrm{AB}}}^2& =(\cos \alpha -\sin \beta {)}^2+(\sin \alpha -\cos \beta {)}^2\\ & =2-2\cos \alpha \sin \beta -2\sin \alpha \cos \beta \end{array}$$

$${\mathrm{A}}^{\prime }(\cos (\alpha +\beta ),\sin (\alpha +\beta )),{\mathrm{B}}^{\prime }(0,1)$$

$$\begin{array}{rl}{\overline{{\mathrm{A}}^{\prime }{\mathrm{B}}^{\prime }}}^2& ={\cos }^2(\alpha +\beta )+(\sin (\alpha +\beta )-1{)}^2\\ & =2-2\sin (\alpha +\beta )\end{array}$$

$$\therefore 2-2\cos \alpha \sin \beta -2\sin \alpha \cos \beta =2-2\sin (\alpha +\beta )$$

$$\therefore \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$

 

$\tan$에 대해서는 특별히 직관적인 방법을 찾지 못했습니다.

$$\tan \theta =\frac{\sin \theta }{\cos \theta }$$

임을 이용합니다.

$$\begin{array}{rl}\tan (\alpha +\beta )& =\frac{\sin (\alpha +\beta )}{\cos (\alpha +\beta )}\\ & =\frac{\sin \alpha \cos \beta +\cos \alpha \sin \beta }{\cos \alpha \cos \beta -\sin \alpha \sin \beta }& \text{divide both sides by }\cos \alpha \cos \beta \\ & =\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }\end{array}$$

 

따라서,

$$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$

$$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$$

$$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$$

이때 증명 방법에 따라 $\alpha$와 $\beta$의 크기에 대해 일반적으로 위

 

이때, $\sin$과 $\cos$에 대한 덧셈 정리는 $0<\alpha ,\beta$, $\alpha +\beta <{90}^{\circ }$일 때 다른 방법으로도 보일 수 있습니다.

 

 $\overline{\mathrm{AB}}=1$이고 직사각형 $◻\mathrm{AXYZ}$에 내접하는 $\mathrm{\angle }\mathrm{ACB}={90}^{\circ }$인 직각 삼각형 $\mathrm{△}\mathrm{ABC}$입니다.

$$\mathrm{\angle }\mathrm{XAC}+\mathrm{\angle }\mathrm{XCA}=\mathrm{\angle }\mathrm{XCA}+\mathrm{\angle }\mathrm{YCB}={90}^{\circ }$$

$$\therefore \mathrm{\angle }BCY=\alpha$$

$$\mathrm{\angle }\mathrm{ABZ}=\mathrm{\angle }\mathrm{BAX}=\alpha +\beta$$

$$\overline{\mathrm{AC}}=\cos \beta ,\overline{\mathrm{BC}}=\sin \beta$$

$$\begin{array}{rl}\overline{\mathrm{AX}}& =\overline{\mathrm{AC}}\sin \alpha \\ & =\cos \beta \cos \alpha \end{array}$$

$$\begin{array}{rl}\overline{\mathrm{BY}}& =\overline{\mathrm{BC}}\sin \alpha \\ & =\sin \beta \sin \alpha \end{array}$$

$$\begin{array}{rl}\therefore \cos (\alpha +\beta )& =\overline{\mathrm{BZ}}\\ & =\overline{\mathrm{AX}}-\overline{\mathrm{BY}}\\ & =\cos \alpha \cos \beta -\sin \alpha \sin \beta \end{array}$$

$$\therefore \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$$

$$\begin{array}{rl}\overline{\mathrm{CX}}& =\overline{\mathrm{AC}}\sin \alpha \\ & =\cos \beta \sin \alpha \end{array}$$

$$\begin{array}{rl}\overline{\mathrm{CY}}& =\overline{\mathrm{BC}}\cos \alpha \\ & =\sin \beta \cos \alpha \end{array}$$

$$\begin{array}{rl}\therefore \sin (\alpha +\beta )& =\overline{\mathrm{AZ}}\\ & =\overline{\mathrm{CX}}+\overline{\mathrm{CY}}\\ & =\sin \alpha \cos \beta +\cos \alpha \sin \beta \end{array}$$

$$\therefore \sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$

 

 $\sin (\alpha +\beta )$와 $\cos (\alpha +\beta )$에 대해 같은 식을 얻었습니다.